reading-notes

Stacks and Queues

Stacks

A stack is a linear data structure that stores items in a Last-In/First-Out (LIFO) or First-In/Last-Out (FILO) manner.

FILO Concept

This means that the first item added in the stack will be the last item popped out of the stack.

LIFO Concept

This means that the last item added to the stack will be the first item popped out of the stack.

Stack methods and operations:

Push : adds node to the stack
Pop: remove nodes from the stack
Top: top node of a stack
Peek: top node’s value in a stack
IsEmpty: returns a boolean (true: when the stack is empty)

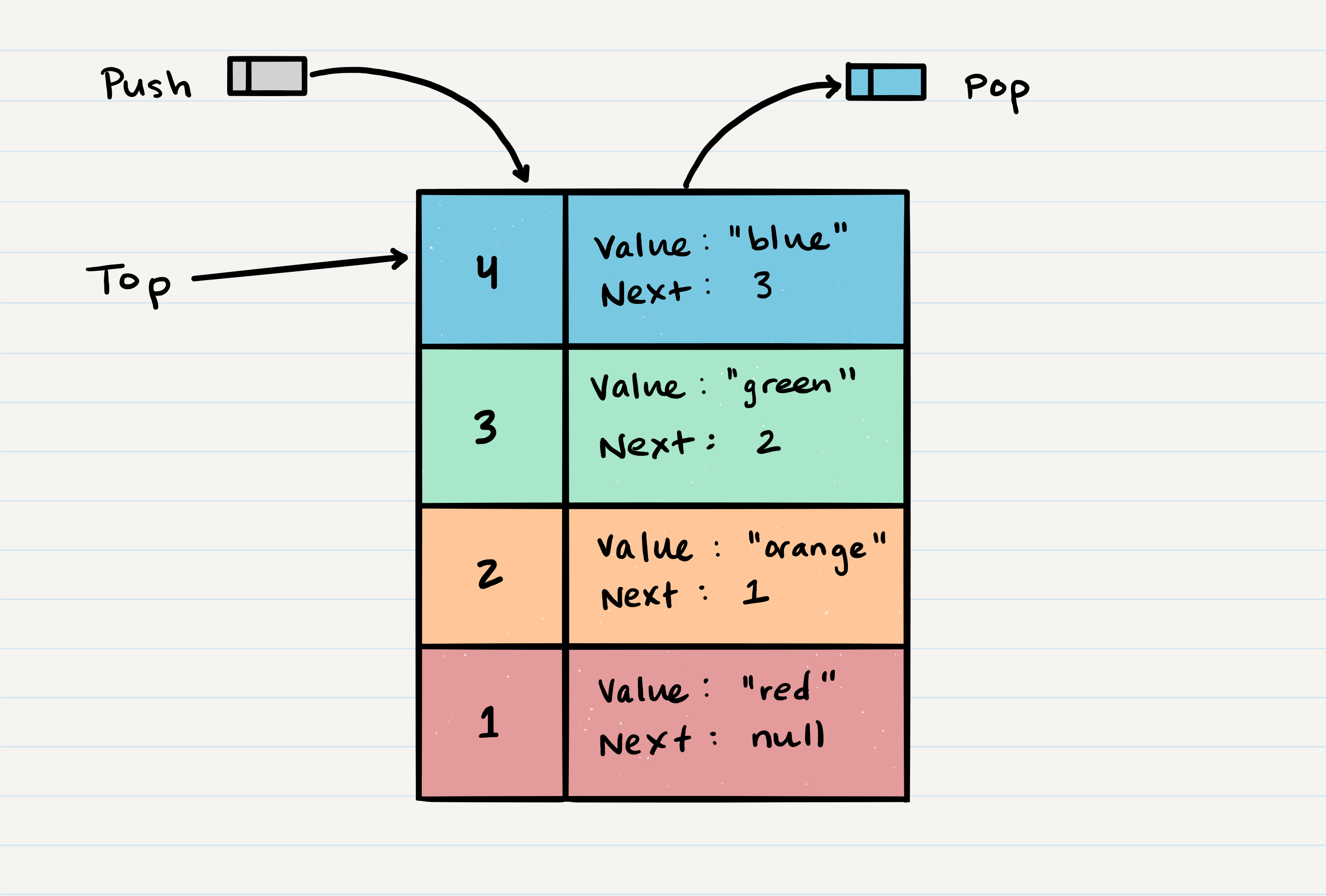
Stack Visual

stack

the picture above shows the structure of a stack,the top is last node pushed into the stack and the first node that would be popped out, if it’s popped out, the top of a stack will be top.next

Stack methods and time complexity

Push

pushing a node into a stack will always have a constant time complexity or O(1), because it will always take the same amount of time no matter what

Pop

pop also has a constant time complexity, because you will always remove from the top, there is no loops.

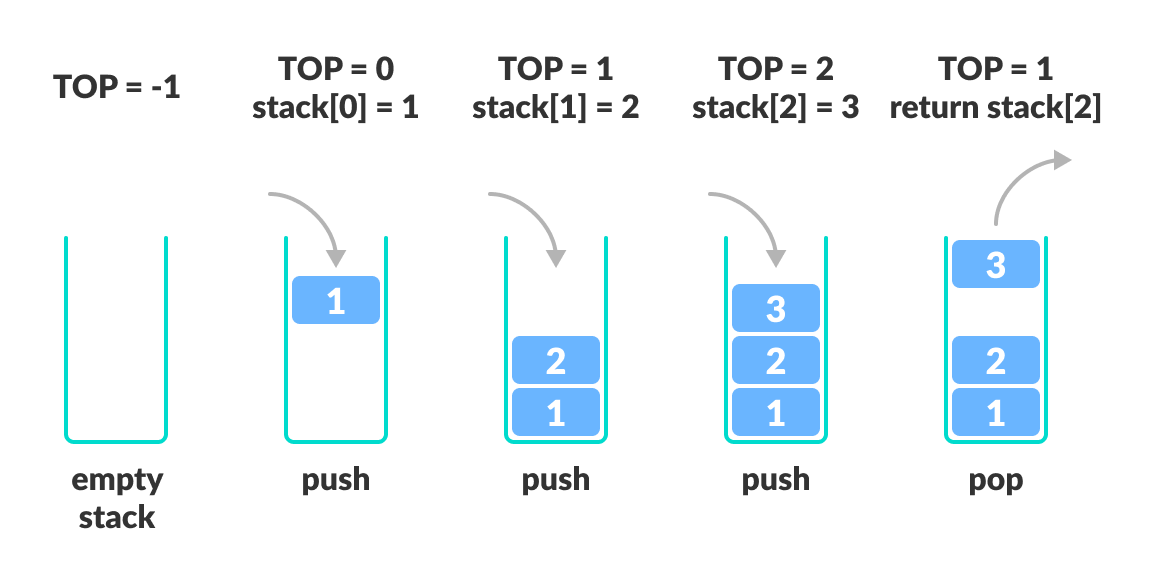
pushandpop

it’s always better to check if the stack empty by using isEmpty() method before using pop, so an exception will be raised if there is no nodes to remove in the stack.

Pseudo code for pop

ALGORITHM pop()

// INPUT <-- No input

// OUTPUT <-- value of top Node in stack

// EXCEPTION if stack is empty

Node temp <-- top

top <-- top.next

temp.next <-- null

return temp.value

### Peek Method

peek returns the value inside the top of the stack Typically, you would check isEmpty before conducting a peek. This will ensure that an exception is not raised.

Pseudo code for peek

ALGORITHM peek()

// INPUT <-- none

// OUTPUT <-- value of top Node in stack

// EXCEPTION if stack is empty

return top.value

### isEmpty method

the time complexity for this method is O(1) // constant

Pseudo code for peek

ALGORITHM isEmpty()

// INPUT <-- none

// OUTPUT <-- boolean

return top = NULL

How can we implement a stack in Python?

*there are two ways for implementing stack in python, which are:

Using the built-in List data structure. Python’s built-in List data structure comes with methods to simulate both and operations.
Using the deque library which efficiently provides stack and queue operations in one object.

Queue

queue is a linear data structure that stores items in First In First Out (FIFO) manner. With a queue the least recently added item is removed first.

Queue concepts

FIFO

This means that the first item in the queue will be the first item out of the queue.

LILO

This means that the last item in the queue will be the last item out of the queue.

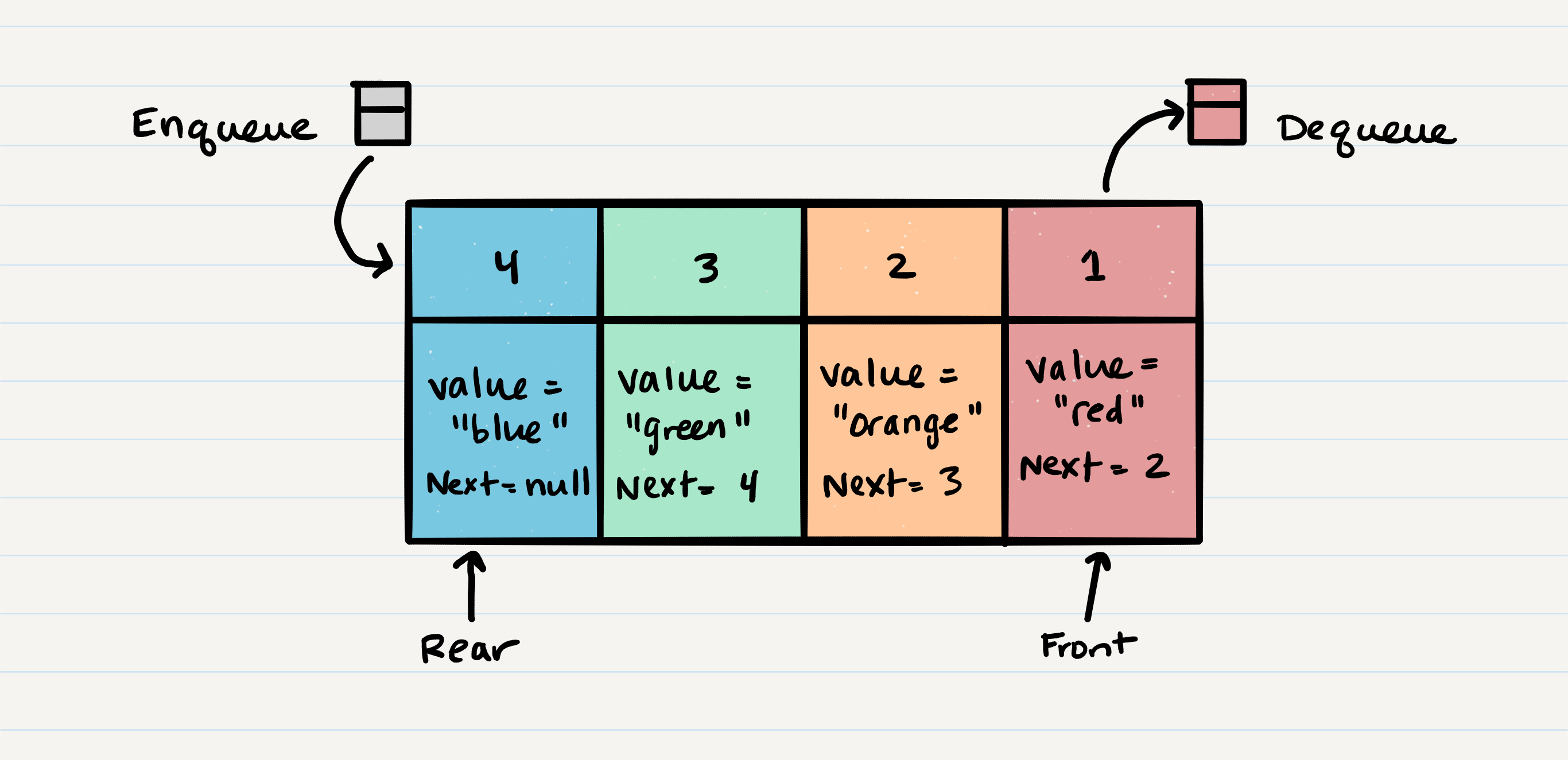
Queue Visualization

the following picture shows the structure of a queue

queue

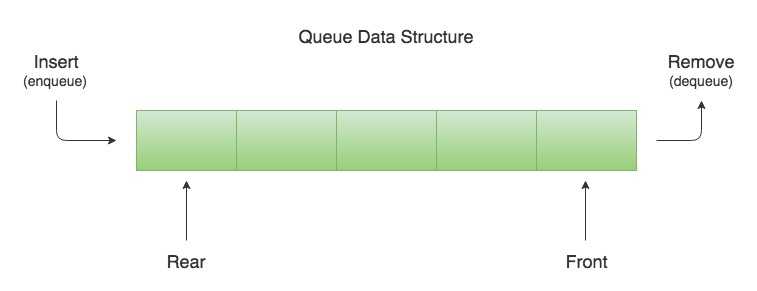
Queue methods and operations

Enqueue: add nodes to the queue
Dequeue: remove nodes from a queue
Front: first Node of the queue.
Rear: last Node of the queue.
Peek: the value inside the first node in a queue
IsEmpty: returns true when queue is empty otherwise returns false.

Enqueue and Dequeue

these two methods will always have a constant time complexity because you will always add or remove the first node .

enqueueanddequeue

ALGORITHM enqueue(value)

// INPUT <-- value to add to queue (will be wrapped in Node internally)

// OUTPUT <-- none

node = new Node(value)

rear.next <-- node

rear <-- node

ALGORITHM dequeue()

// INPUT <-- none

// OUTPUT <-- value of the removed Node

// EXCEPTION if queue is empty

Node temp <-- front

front <-- front.next

temp.next <-- null

return temp.value

### Peek

When conducting a peek, you will only be inspecting the front Node of the queue.
Typically, you want to check isEmpty before conducting a peek. This will ensure that an exception is not raised.
big O of time for peek is O(1) // constant

ALGORITHM peek()

// INPUT <-- none

// OUTPUT <-- value of the front Node in Queue

// EXCEPTION if Queue is empty

return front.value

IsEmpty

Time complexity // O(1)

ALGORITHM isEmpty()

// INPUT <-- none

// OUTPUT <-- boolean

return front = NULL

Applications of Queue Data Structure

When a resource is shared among multiple consumers.
When data is transferred asynchronously (data not necessarily received at same rate as sent) between two processes. 3) In Operating systems:

4) In Networks:

   a) Queues in routers/ switches 
   b) Mail Queues

5) Variations